In my research, there are many problems involve networks of different types, e.g. social network, online-trading networks, crowd-sourcing, etc. I was so happy to find a new powerful tool for my research, the graph convolutional network, which applies deep learning on graph structures.
Graph convolutional network (GCN)
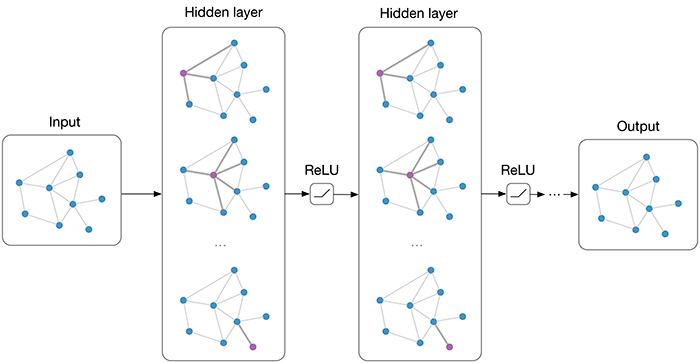
There is currently no official definition for GCN. As most graph neural network models have a somewhat universal architecture in common. Thomas referred to the using convolution on graph-liked structures as graph convolutional neural network.
For these models, the goal is then to learn a function of signals/features on a graph 
which takes as input:
A feature description 
latex N×D \) feature matrix 
latexN×F\) feature matrix, where 
latexN \times D \)) to the new output that somehow reserves the structure of the original graph. The process is called graph autoencoder.
The ipynb below illustrates graph embedding. Please note that the dataset contains no node feature. That makes our model much simpler than ones in reality, such as transaction networks, citation networks.
