One way to get a diverse set of classifiers is to use very different training algorithms,
as just discussed. Another approach is to use the same training algorithm for every
predictor but to train them on different random subsets of the training set. When
sampling is performed with replacement, this method is called bagging
(short for bootstrap aggregating). When sampling is performed without replacement, it is called pasting.
Sampling with replacement:
Consider a population of potato sacks, each of which has either 12, 13, 14, 15, 16, 17, or 18 potatoes, and all the values are equally likely. Suppose that, in this population, there is exactly one sack with each number. So the whole population has seven sacks. If I sample two with replacement, then I first pick one (say 14). I had a 1/7 probability of choosing that one. Then I replace it. Then I pick another. Every one of them still has 1/7 probability of being chosen.
And there are exactly 49 different possibilities here (assuming we distinguish between the first and second.) They are: (12,12), (12,13), (12, 14), (12,15), (12,16), (12,17), (12,18), (13,12), (13,13), (13,14), etc.
Sampling without replacement:
Consider the same population of potato sacks, each of which has either 12, 13, 14, 15, 16, 17, or 18 potatoes, and all the values are equally likely. Suppose that, in this population, there is exactly one sack with each number. So the whole population has seven sacks. If I sample two without replacement, then I first pick one (say 14). I had a 1/7 probability of choosing that one. Then I pick another. At this point, there are only six possibilities: 12, 13, 15, 16, 17, and 18.
So there are only 42 different possibilities here (again assuming that we distinguish between the first and the second.) They are: (12,13), (12,14), (12,15), (12,16), (12,17), (12,18), (13,12), (13,14), (13,15), etc.
What’s the Difference?
When we sample with replacement, the two-sample values are independent. Practically, this means that what we get on the first one doesn’t affect what we get on the second. Mathematically, this means that the covariance between the two is zero.
In sampling without replacement, the two-sample values aren’t independent. Practically, this means that what we got on for the first one affects what we can get for the second one. Mathematically, this means that the covariance between the two isn’t zero. That complicates the computations. In particular, if we have an SRS (simple random sample) without replacement, from a population with variance 
, then the covariance of two of the different sample values is 
, where N is the population size.
Population size
When we sample without replacement and get a non-zero covariance, the covariance depends on the population size. If the population is very large, this covariance is very close to zero. In that case, sampling with replacement isn’t much different from sampling without replacement. In some discussions, people describe this difference as sampling from an infinite population (sampling with replacement) versus sampling from a finite population (without replacement).
Examples with Scikit-learn
For convenience, we use moon data from a generator in sklearn:
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=500, noise=0.30, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)Create a classifier using BaggingClassifier from sklearn
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
bag_clf = BaggingClassifier(
DecisionTreeClassifier(), n_estimators = 500,
max_samples=100, bootstrap=True, n_jobs = -1
)
bag_clf.fit(X_train, y_train)
y_pred = bag_clf.predict(X_test)Create another normal decision tree classifier:
tree_clf = DecisionTreeClassifier(random_state=42)
tree_clf.fit(X_train, y_train)
y_pred_tree = tree_clf.predict(X_test)
print(accuracy_score(y_test, y_pred_tree))Visualise the decision boundary
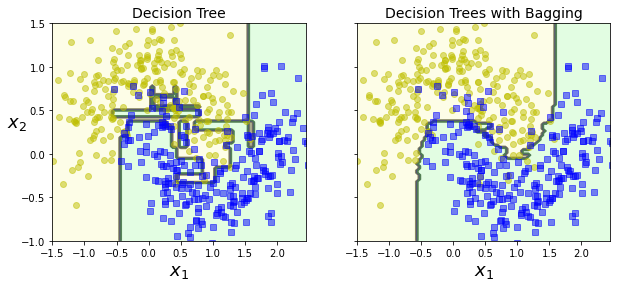
As you can see, the ensemble’s predictions will likely generalize much better than the single Decision Tree’s predictions: the ensemble has a comparable bias but a smaller variance (it makes roughly the same number of errors on the training set, but the decision boundary is less irregular).
Overall, bagging often results in better models, which explains why it is generally preferred. However, if you have spare time and CPU power you can use cross-validation to evaluate both bagging and pasting and select the one that works best.
For other sampling methods, please visit here.