The most basic yet important thing when working with data array is its dimensions. This article will cover several data shapes and reshaping techniques.
Why need reshaping data
Imagine that you are starving and suddenly given a piece of delicious food. You may try to put it all in your mouth (Fig 1a) and find out it cannot help your hunger. So, you decided to arrange your food so that it not only fits your mouth but also you can eat really fast (Fig 1b).
That is it! In machine learning, especially, when working with a neural network, reshaping data is to make sure that the dimension of a data slice is suitable to process.
A typical example is matrix multiplication, e.g. matmul operator in TensorFlow or Numpy. Revise that 
is valid only when the width of matrix A (number of columns) equals the height of matrix B (number of rows).
Sample code with TensorFlow 2.0:
%tensorflow_version 2.x
import tensorflow as tf
# 1-D tensor `A` = [1, 2, 3] (dimensions 1 x 3)
A = tf.constant([[1, 2, 3]])
# 1-D tensor `B` = [4, 5, 6] (dimensions 1 x 3)
B = tf.constant([[ 4, 5, 6]])
# C = A x B
C = tf.matmul(A, B)If you try to execute the code, you will get an error “Matrix size-incompatible” because both A and B are sized as 1 x 3.
#InvalidArgumentError: Matrix size-incompatible: In[0]: [1,3], In[1]: [1,3] [Op:MatMul] name: MatMul/To fix that, change the shape of B to 3×1 as follow.
B = tf.constant([[ 4, 5, 6]], shape=[3, 1])Data Shapes
(n, ) shape
This is a very common shape of 1-D array but may confuse many beginners. A shape attribute returns a tuple of the length of each dimension of the array. There is nothing after the comma because there is only ONE INDEX to identify elements.
i= 0 1 2 3 4 5
┌───┬───┬───┬───┬───┬───┐
│ 0 │ 1 │ 2 │ 3 │ 4 │ 5 │
└───┴───┴───┴───┴───┴───┘# Code with Numpy
from numpy import array
# define array
data = array([1, 2, 3, 4])
print(data.shape)
#output:
(4, )# Code with TensorFlow
A = tf.constant([1, 2, 3])
print(A.shape)
#output:
(3, )
You may wonder if there is a (, n) shape? No, I never see one like that except in this article. 😀 .
(1, n) shape
Again, many may ask what is the difference between (n, ) vs (1, n). They are both 1-D but the former is array while the latter is a matrix (with 1 row and n columns). Namely, there are two indices associated with an element. This shape is also known as a row vector.
i= 0 1 2 3 4 5
j= 0 0 0 0 0 0
┌────┬────┬────┬────┬────┬────┐
│ 0 │ 1 │ 2 │ 3 │ 4 │ 5 │
└────┴────┴────┴────┴────┴────┘# Code with Numpy
from numpy import array
# define 2D array in [[ data ]]
data = array([[1, 2, 3, 4]])
print(data.shape)
#output:
(1, 4)# Code with TensorFlow
A = tf.constant([[1, 2, 3]])
print(A)
#output
tf.Tensor([[1 2 3]], shape=(1, 3), dtype=int32)
(n, 1) shape
Nothing special, this shape has n rows and 1 column. Nevertheless, this shape is very important as a column vector. Conveniently, we can use the transpose operator (T in numpy and tf.transpose in TF) to create a column vector from a row vector.
# Code with Numpy
from numpy import array
# define 2D array in [[ data ]]
data = array([[1, 2, 3, 4]]).T
print(data.shape)
#output:
(4, 1)# Code with TensorFlow
data = tf.constant([[1, 2, 3]])
data_t = tf.transpose(data)
print(data_t.shape)
#output
(3, 1)(m, n) shape
This shape has m rows and n columns. There are several ways to create data of this shape.
# Code with Numpy
# define 2D m x n array in [[ data ]]
data = array([
[1, 2, ..., n]
...
[m, m1, ..., mn]
])# Code with TensorFlow
A = tf.constant([
[1, 2, ..., n]
...
[m, m1, ..., mn]
])If you already have m rows of n elements, we can form a matrix of 
by using vstack .
# Code with Numpy
a = np.array([1, 2, 3])
b = np.array([2, 3, 4])
np.vstack((a,b))
#output
#array([[1, 2, 3],
[2, 3, 4]])# Code with TensorFlow 2.0
x = tf.constant([1, 4])
y = tf.constant([2, 5])
tf.stack([x, y])
#output
# [[1, 4], [2, 5]] (Pack along first dim.)Reshape a shape to (almost) any other shape
You can use reshape function to transform a specific shape to another. If you want to transform from to k dimensional data of shape 
to h dimensional data of shape 
.
Condition: 
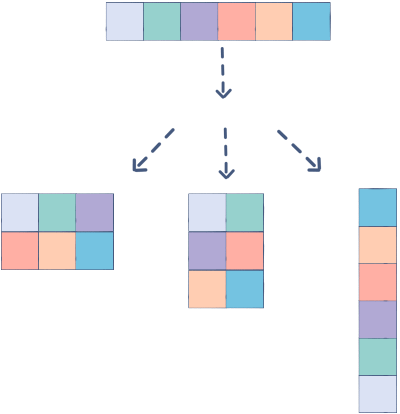
The sample code below demonstrates different shapes transformation: (4, ) -> (2, 2) -> (2, 1, 1, 2) -> (1, 2, 2).
from numpy import array
import numpy as np
data = array([1, 2, 3, 4])
data22 = data.reshape(2,2)
data2112 = np.reshape(data22, (2, 1, 1, 2))
data211 = data2112.reshape(1,2,2)
#print output:
print(data)
print(data22)
print(data2112)
print(data211)import tensorflow as tf
data = tf.constant([1, 2, 3, 4])
data22 = tf.reshape(data, [2,2])
data2112 = tf.reshape(data22, (2, 1, 1, 2))
data211 = tf.reshape(data2112,(1,2,2))
#print output
print(data.numpy())
print(data22.numpy())
print(data2112.numpy())
print(data211.numpy())#output data
[1 2 3 4]
#data22--------------------
[[1 2]
[3 4]]
#data2112------------------
[[[[1 2]]]
[[[3 4]]]]
#data211--------------------
[[[1 2] #
[3 4]]]Quickly flatten data
To transform an array to 1-d :
# Code with Numpy
a = np.array([[1,2], [3,4]])
a.flatten()
#output
array([1, 2, 3, 4])# Code with TensorFlow 2.0
a = tf.constant([[1,2],[3,4]])
a = tf.reshape(a, [-1])
print(a.numpy())
#output
array([1, 2, 3, 4])Conclusion
Good control of the shapes of your data is the first step to avoid many errors related to array/matrix operations. There are also other ways to reshape your data. Find more numpy indexing, hstack, data indexing and slicing (with pandas, or TensorFlow)
Happy reshaping! 😀
