Number of Islands solution

In this post, we have a look at using a queue and breath-first search algorithm to solve a Leetcode challenge. The problem is stated as follows.

Given an m x n 2D binary grid grid which represents a map of '1's (land) and '0's (water), return the number of islands.

An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.

Example 1:

Input: grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
Output: 1

Queue and BFS

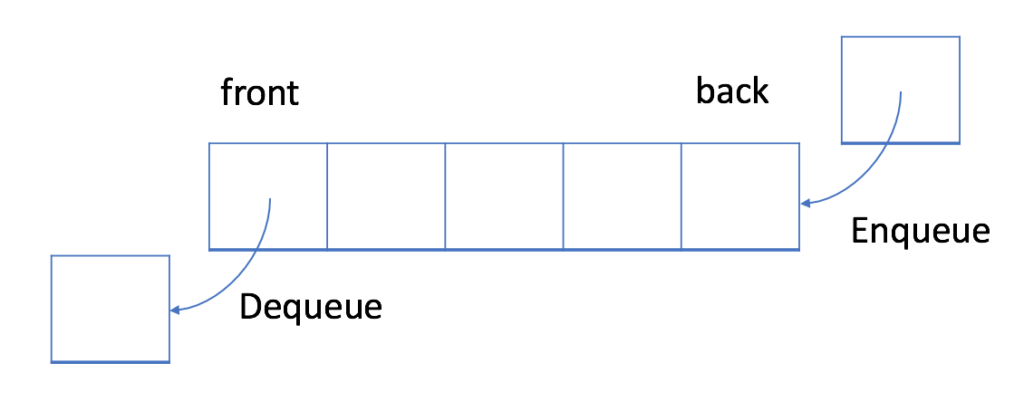
In a FIFO data structure, the first element added to the queue will be processed first.

As shown in the picture above, the queue is a typical FIFO data structure. The insert operation is also called enqueue and the new element is always added at the end of the queue. The delete operation is called dequeue. You are only allowed to remove the first element.

Solution with bfs

The purpose of the breadth-first search is to write down all the branches when facing a junction and then choose one of them to enter, Then record its shunting situation, and then return to another fork, and repeat the operation.

The pseudo-code looks like this:

 1  procedure BFS(G, root) is
 2      let Q be a queue
 3      label root as explored
 4      Q.enqueue(root)
 5      while Q is not empty do
 6          v := Q.dequeue()
 7          if v is the goal then
 8              return v
 9          for all edges from v to w in G.adjacentEdges(v) do
10              if w is not labeled as explored then
11                  label w as explored
12                  Q.enqueue(w)

Kotlin implementation

class Solution {
    fun numIslands(grid: Array<CharArray>): Int {
        //BFS
        //find 1 and expands until there is no more 1 connected horizontally and vertically
        //increase by 1
        var result = 0
        val queue: Queue<Pair<Int, Int>> = LinkedList<Pair<Int, Int>>()

        for(r in grid.indices){
            for (c in grid[0].indices){
                if(grid[r][c] == '1'){
                    result += 1
                    queue.add(Pair(r, c))
                    
                    grid[r][c] = '0' //visited
                    
                    while(!queue.isEmpty()){
                        val (x, y) = queue.poll()
                        
                        if(x > 0 && grid[x-1][y] == '1') //compare the left
                        {
                            grid[x-1][y] = '0'
                            queue.add(Pair(x-1, y))
                        }
                        if(x < grid.lastIndex && grid[x+1][y] == '1') //compare the right
                        {
                            grid[x+1][y] = '0'
                            queue.add(Pair(x+1, y))
                        }
                        if(y > 0 && grid[x][y - 1] == '1') //compare the top
                        {
                            grid[x][y - 1] = '0'
                            queue.add(Pair(x, y - 1))
                        }
                        if(y < grid[0].lastIndex  && grid[x][y + 1] == '1') //compare the bottom
                        {
                            grid[x][y + 1] = '0'
                            queue.add(Pair(x, y + 1))
                        }
                       
                    }
                }
            }
        }
        
        return result
    }
}

For more algorithm articles, please go here.